Equipotency and (in)finiteness

Naive set theory: Size of a set

Equipotency and (in)finiteness

We call the set \(X\) equipotent or equinumerous with respect to the set \(Y\), and we also say that \(X\) has the same cardinality or the same number of elements as \(Y\) if there exists a bijection \(f\:\;X\rightarrow Y\). We denote this as \(X\cong Y\). If two sets \(X\) and \(Y\) are not equipotent, we denote this with \(X\ncong Y\).

The relation "is equipotent to" is an equivalence relation between sets. This means that for arbitrary sets \(X\), \(Y\), and \(Z\):

\(X\cong X\);
If \(X\cong Y\), then \(Y\cong X\);
If \(X\cong Y\) and \(Y\cong Z\), then \(X\cong Z\).

\(X\cong X\) (reflexivity): the identity function \(\mathrm{id}_X:\;X\rightarrow X\) defined by \(\mathrm{id}(x)=x\) for all \(x\in X\) is a bijection;
If \(X\cong Y\), then \(Y\cong X\) (symmetry): if \(f\:\;X\rightarrow Y\) is a bijection, then the inverse function \(f^{-1}\:\;Y\rightarrow X\) is also that;
If \(X\cong Y\) and \(Y\cong Z\), then \(X\cong Z\) (transitivity): if \(f\:\;X\rightarrow Y\) is a bijection and \(g\:\;Y\rightarrow Z\) is a bijection, then the composition \(g\circ f\:\;X\rightarrow Z\) is also a bijection.

Examples

\(\{a,b,c\}\cong \{1,2,3\}\)
because the function \(f\) defined by \(f(a)=1\), \(f(b)=2\), \(f(c)=3\) is a bijection from \(\{a,b,c\}\) to \(\{1,2,3\}\).
\(\{a,b,c,d\}\ncong \{1,2,3\}\)
because the pigeonhole principle guarantees that there is no injective function from \(\{a,b,c,d\}\) to \(\{1,2,3\}\), let alone a bijection.
The closed interval \([0,1]\) in \(\mathbb{R}\) is equipotent to any other closed interval \([a,b]\) (with \(a<b\))
because the function \(f\) defined by \(f(x)=(b-a)x+a\) is a bijection from \([0,1]\) to \([a,b]\).
The open interval \((-1,1)\) is equipotent to \(\mathbb{R}\)
because the function \(f:\;(-1,1)\rightarrow \mathbb{R},\quad f(x)=\tan(\tfrac{1}{2}\pi x)\) is a bijectie from \((-1,1)\) to \(\mathbb{R}\).
\(\mathbb{N}\backslash \{0\}\cong \mathbb{N}\)
because the function \(f\) defined by \(f(n)=n-1\) is a bijection from \(\mathbb{N}\backslash \{0\}\) to \(\mathbb{N}\). This means that when counting elements, it does not matter whether you start at \(1\) or \(0\).
\(\mathbb{Z}\cong \mathbb{N}\) because the function \(f(n)=\begin{cases}2n&\text{if }n\ge 0\\ -2n-1&\text{if }n< 0\end{cases}\) is a bijection from \(\mathbb{Z}\) to \(\mathbb{N}\).

A formal definition of finiteness and infiniteness of a set is as follows:

A set \(X\) is called

finite if there exists an \(n\in \mathbb{N}\) such that \(X\cong\{0,\ldots , n-1\}\) (where \(\{\}=\emptyset\)).
The number of elements of \(X\), which we elegantly call the cardinality of \(X\), is then equal to \(n\) and we denote this as \(|X|=n\);
infinite if \(X\) is not finite.
Examples of infinite sets are the number sets \(\mathbb{N}\), \(\mathbb{Z}\), \(\mathbb{Q}\), and \(\mathbb{R}\)

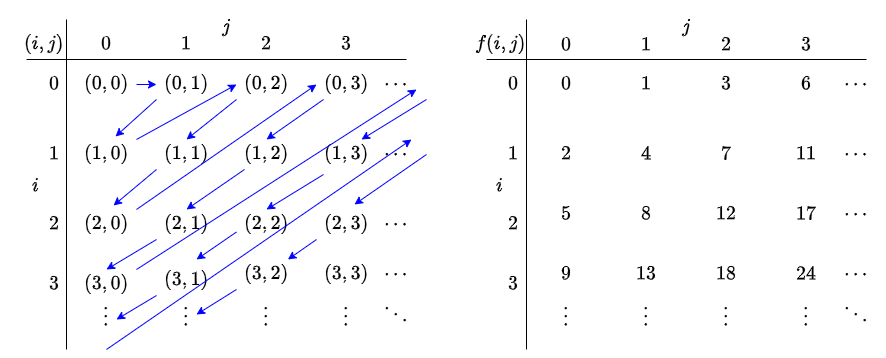
\(\mathbb{N}\times \mathbb{N} \cong \mathbb{N}\)

In the diagram below, the elements of \(\mathbb{N}\times \mathbb{N}\) are shown on the left in a grid along with blue arrows indicating the order in which we will traverse the elements of the set. On the right is the counting of the elements according to this traversal along diagonals starting from \(0\).

traversal along diagonals

At position \((i,j)\) we arrive with the count number given by the function \(f\) defined by \(f(i,j)=\tfrac{1}{2}(i+j)(i+j+1)+i\). This is a bijection from \(\mathbb{N}\times \mathbb{N}\) to \(\mathbb{N}\).

Without proof:

\(\mathbb{R} \cong {\Large\wp}(\mathbb{N})\).