Oplossen van een eerstegraadsongelijkheid door herleiding

Lineaire vergelijkingen en ongelijkheden oplossen: Eerstegraadsongelijkheden met één onbekende

Oplossen van een eerstegraadsongelijkheid door herleiding

De stappen in het oplossen van een eerstegraadsongelijkheid met één onbekende door herleiding zijn dezelfde als bij het oplossen van een eerstegraadsvergelijking door herleiding:

aan beide zijden dezelfde term optellen of aftrekken;
beide zijden met hetzelfde getal ongelijk aan nul vermenigvuldigen of delen;
gelijksoortige termen samenvoegen.

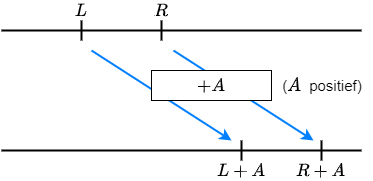
$L<R$ is gelijkwaardig met
$L+A<R+A$ en met $L-A<R-A$

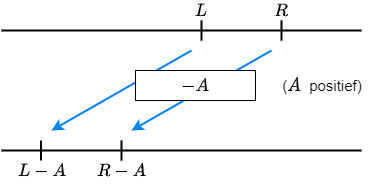
$L>R$ is gelijkwaardig met
$L+A>R+A$ en met $L-A>R-A$

Hierbij is $A$ een willekeurige uitdrukking.

Voorbeeld
$\begin{aligned} 2x+3&>4\\[0.25cm] 2x+3-3&>4-3\\[0.25cm] 2x&>1\end{aligned}$

Ongelijkheden met ≤ of ≥ De regel geldt ook voor ongelijkheden met $\le$ of $\ge$ ; in feite gaat het hierbij om een samenstelling van een ongelijkheid met $\lt$ of $\gt$ en een eerstegraadsvergelijking, waarvoor de regel ook geldt. Bijvoorbeeld: $\begin{aligned} 2x+3&\ge4\\[0.25cm] 2x+3-3&\ge4-3\\[0.25cm] 2x&\ge 1\end{aligned}$

Wel of geen equivalentiesymbool De herleiding is gebaseerd op equivalentie van ongelijkheden en het gebruik van equivalentiesymbool $\Leftrightarrow$ is dus toepasselijk. Je schrijft dan in het voorbeeld $\begin{aligned} 2x+3>4 &\Leftrightarrow 2x+3-3>4-3\\[0.25cm] &\Leftrightarrow2x>1\end{aligned}$ Maar door de stapsgewijze, gestructureerde herleiding wordt vaak volstaan met het plaatsen van opeenvolgende equivalente uitdrukkingen op aparte regels, met weglating van het equivalentiesymbool. Je krijgt dan dus $\begin{aligned} 2x+3&>4\\[0.25cm] 2x+3-3&>4-3\\[0.25cm] 2x&>1\end{aligned}$

Visualisatie Als je voor $x$ in de ongelijkheid $L<R$ een oplossing invult, dan worden $L$ en $R$ getallen waarbij $L$ links van $R$ ligt op de getallenlijn. Als je bij beide getallen $A$ optelt of aftrekt verandert er niets aan de onderlinge positie.

Als $A>0$ , dan is $L<R$ is gelijkwaardig met
$A\cdot L<A\cdot R$ en met $\dfrac{L}{A}<\dfrac{R}{A}$

Als $A>0$ , dan is $L>R$ is gelijkwaardig met
$A\cdot L>A\cdot R$ en met $\dfrac{L}{A}>\dfrac{R}{A}$

Als $A<0$ , dan is $L<R$ is gelijkwaardig met
$A\cdot L>A\cdot R$ en met $\dfrac{L}{A}>\dfrac{R}{A}$

Als $A<0$ , dan is $L>R$ is gelijkwaardig met
$A\cdot L<A\cdot R$ en met $\dfrac{L}{A}<\dfrac{R}{A}$

Hierbij is $A$ een willekeurig getal ongelijk aan nul.

Voorbeelden
$\begin{aligned} -x&< 1\\[0.25cm] (-1)\cdot (-x)&\gt(-1)\cdot 1\\[0.25cm] x&\gt -1\\[0.75cm]-2x&>4\\[0.25cm]\dfrac{-2x}{-2}&<\dfrac{4}{-2}\\[0.25cm] x&<2\end{aligned}$

Ongelijkheden met kleiner (groter) dan of gelijk aan De regel geldt ook voor ongelijkheden met $\le$ of $\ge$ ; in feite gaat het hierbij om een samenstelling van een ongelijkheid met $\lt$ of $\gt$ en een eerstegraadsvergelijking, waarvoor de regel ook geldt.
Dus bij vermenigvuldigen met of delen door een negatief getal wordt het vergelijkingsteken $\le$ vervangen door $\ge$ en wordt $\ge$ vervangen door $\le$ ; het vergelijkingsteken klapt als het ware om. Bijvoorbeeld: $\begin{aligned} -x&\le 1\\[0.25cm] (-1)\cdot (-x)&\ge(-1)\cdot 1\\[0.25cm] x&\ge -1\\[0.75cm]-2x&\ge4\\[0.25cm]\dfrac{-2x}{-2}&\le\dfrac{4}{-2}\\[0.25cm] x&\le2\end{aligned}$

Visualisatie

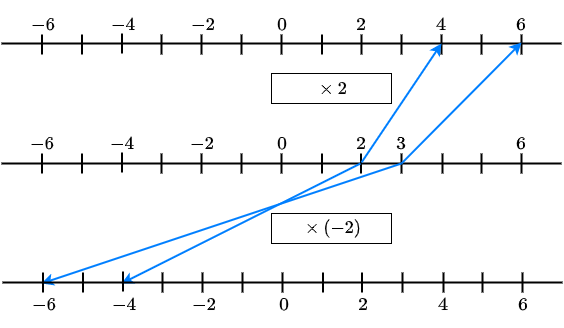
Als je voor $x$ in de ongelijkheid $L<R$ een oplossing invult, dan worden $L$ en $R$ getallen waarbij $L$ links van $R$ ligt op de getallenlijn. Als je beide getallen vermenigvuldigt met een getal $A$ of deelt door $A$ , hangt het van het teken van $A$ af of de onderlinge positie op de getallenlijn wel of niet verandert.

Stel bijvoorbeeld dat je na substitutie van $x$ uitkomt op $L=2$ en $R=3$ . Dan geldt dus $L<R$ en ligt $L$ links van $R$ ligt op de getallenlijn. Als je in de ongelijkheid links en recht vermenigvuldigt met $2$ , krijg je $4<6$ en dat is waar. Maar had je in plaats daarvan links en rechts in de ongelijkheid met $-2$ vermenigvuldigt, dan krijg je $-4<-6$ en dat is onjuist; de ware bewering is $-4>-6$ en het vergelijkingsteken 'klapt om' omdat het getal dat eerst het meest links op de getallenlijn lag nu juist het meest rechts komt te liggen.

Met bovenstaande regels kun je lineaire ongelijkheden oplossen, dat wil zeggen herleiden tot ongelijkheden waarin de onbekende geïsoleerd is en links in een ongelijkheid staat.

In het algemeen zijn de oplossingen van $ax+b<0$ met onbekende $x$ als volgt te vinden.

$\;$ geval	$\;$ oplossingen
$\;a>0\;$	$\;x<−\frac{b}{a}\;$
$\;a<0\;$	$\;x>−\frac{b}{a}\;$
$\;a=0$ en $b\ge 0\;$	$\;$ geen oplossing $\;$
$\;a=0$ en $b<0\;$	$\;$ elk reëel getal $x\;$

We geven aan waarom. De ongelijkheid is $ax+b<0$ .

$\;$ geval	$\;$ oplossingen	$\;$ verklaring
$\;a>0$	$\;x<−\frac{b}{a}\;$	$\;$ Trek links en rechts $b$ af en $\;$ deel vervolgens beide zijden door $a$ .
$\;a<0$	$\;x>−\frac{b}{a}\;$	$\;$ Trek links en rechts $b$ af en $\;$ deel vervolgens beide zijden door $a$ . $\;$ Omdat $a<0$ klapt het teken om
$\;a=0$ en $b\ge 0$	$\;$ geen oplossing	$\;$ De vergelijking wordt $b<0$ en dit is $\;$ niet waar onder de gegeven condities, $\;$ ongeacht de waarde van $x$ .
$\;a=0$ en $b<0$	$\;$ elk reëel getal $x$	$\;$ De vergelijking wordt $b<0$ $\;$ en dit is waar voor elke $x$ $\;$ onder de gegeven condities,.

In plaats van de conclusie dat er geen oplossing van een ongelijkheid is, spreken we ook wel van een lege oplossingsverzameling. Een lege verzameling wordt genoteerd als $\{\}$ or $\emptyset$ .

Bovenstaande regel, en die bij andere ongelijkheidstekens, hoef je niet te onthouden, omdat de oplossingen eenvoudig te vinden zijn door herleiding.

Los exact op: $-7x \ge -2$

$x \le \frac{2}{7}$

Immers: $\begin{aligned} -7x &\ge -2 &\quad \blue{\text{de gegeven ongelijkheid}} \\ \\ \frac{-7x}{-7} &\le \frac{-2}{-7} &\quad \blue{\text{deling door }-7\text{ en omdat }-7<0}\\ &&\quad \blue{\text{klapt het vergelijkingsteken om}} \\ \\ x & \le \frac{2}{7} &\quad\blue{\text{vereenvoudiging}}\end{aligned}$

Nieuw voorbeeld